棋盘游戏（HDOJ 1281）

Problem Description

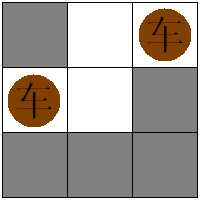
小希和Gardon在玩一个游戏：对一个N*M的棋盘，在格子里放尽量多的一些国际象棋里面的“车”，并且使得他们不能互相攻击，这当然很简单，但是Gardon限制了只有某些格子才可以放，小希还是很轻松的解决了这个问题（见下图）注意不能放车的地方不影响车的互相攻击。
所以现在Gardon想让小希来解决一个更难的问题，在保证尽量多的“车”的前提下，棋盘里有些格子是可以避开的，也就是说，不在这些格子上放车，也可以保证尽量多的“车”被放下。但是某些格子若不放子，就无法保证放尽量多的“车”，这样的格子被称做重要点。Gardon想让小希算出有多少个这样的重要点，你能解决这个问题么？

Input

输入包含多组数据，
第一行有三个数N、M、K(1<N,M<=100 1<K<=N*M)，表示了棋盘的高、宽，以及可以放“车”的格子数目。接下来的K行描述了所有格子的信息：每行两个数X和Y，表示了这个格子在棋盘中的位置。

Output

对输入的每组数据，按照如下格式输出：
Board T have C important blanks for L chessmen.

Sample Input

3 3 4
1 2
1 3
2 1
2 2
3 3 4
1 2
1 3
2 1
3 2

Sample Output

Board 1 have 0 important blanks for 2 chessmen.
Board 2 have 3 important blanks for 3 chessmen.

My Code

这题不放在这个专题还真不一定能想到用二分图，想到了就很简单，按行和列转化成二分图，最大匹配数就是最多能放的车的数量，这题就转化为，删除哪些边会使最大匹配数减小，加个循环就行了。

#include 
#include 

using namespace std;
int n, m, k;
int linker[150];
bool map[150][150];
bool vis[150];
int cnt;
int ans1, ans2;
int tot;
bool dfs(int u)
{
    for (int i = 1; i <= n; i++)
        if (map[u][i] && !vis[i])
        {
            vis[i] = 1;
            if (linker[i] == -1 || dfs(linker[i])) //如果i没有对象或者i的对象还能找到其他对象
            {                                      //那么u和i就匹配
                linker[i] = u;
                return true;
            }
        }
    return false;
}
void hungary()
{
    cnt = 0;
    memset(linker, -1, sizeof(linker));
    for (int i = 1; i <= n; i++)
    {
        memset(vis, false, sizeof(vis)); //因为别人找过的对象你也还可以去试试，所以每次都要清空
        if (dfs(i))                      //如果i能找到对象，匹配数++
            cnt++;
    }
}
int main()
{
    while (cin >> n >> m >> k)
    {
        memset(map, false, sizeof(map));
        for (int i = 0; i < k; i++)
        {
            int u, v;
            cin >> u >> v;              //转化成二分图
            map[u][v] = 1;
        }
        hungary();
        ans1 = cnt;                     //ans1最大匹配数，即最多能放的车
        ans2 = 0;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
            {
                if (map[i][j])
                {
                    map[i][j] = 0;      //若某格子不放车
                    hungary();
                    if (cnt < ans1)     //最大匹配数变小了
                        ans2++;         //说明是重要点
                    map[i][j] = 1;
                }
            }
        cout << "Board " << ++tot << " have " << ans2 << " important blanks for " << ans1 << " chessmen." << endl;
    }
}